- Licensing Information -
No Drawing Block: How to Get Over Obstacles in Drawing by Naoki Saito
Licensing Information
Selling Points
・Offers advice for four major concerns of people who draw pictures: “I can’t draw well,” “I can’t get enough people to see my work,” “I can’t get work,” “I don’t feel motivated.”
・The long-awaited publication of the YouTube channel with over 1.3 million subscribers!
CHAPTER 1: I Can’t Make Progress
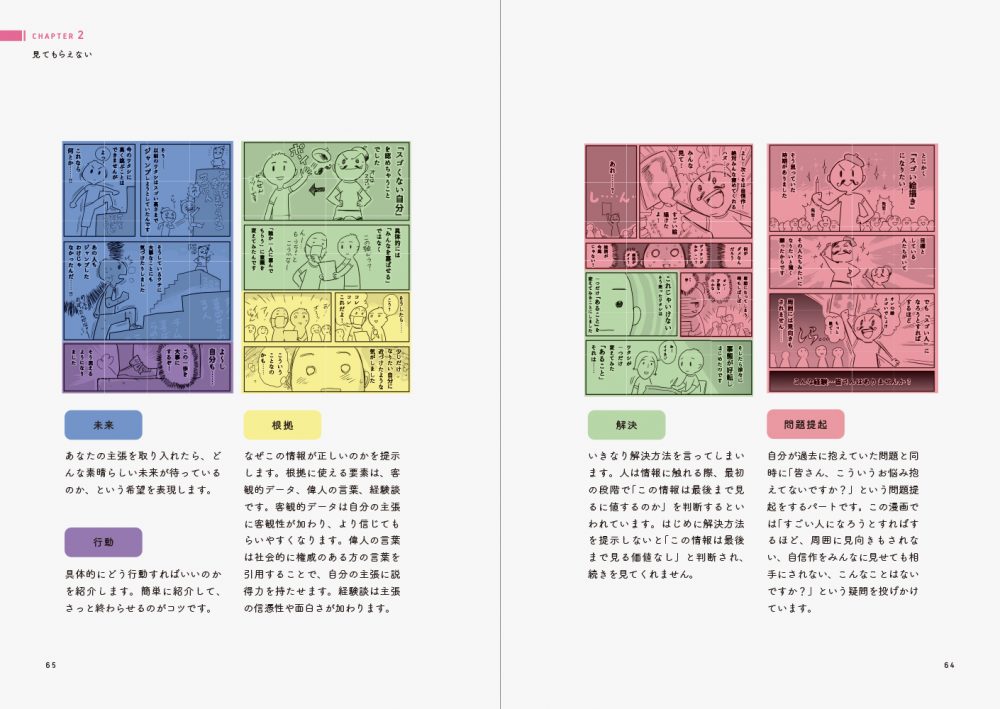
CHAPTER 2: I Can’t Get My Work Seen
CHAPTER 3: I Can’t Get Work
CHAPTER 4: Anyway, I Can’t Draw
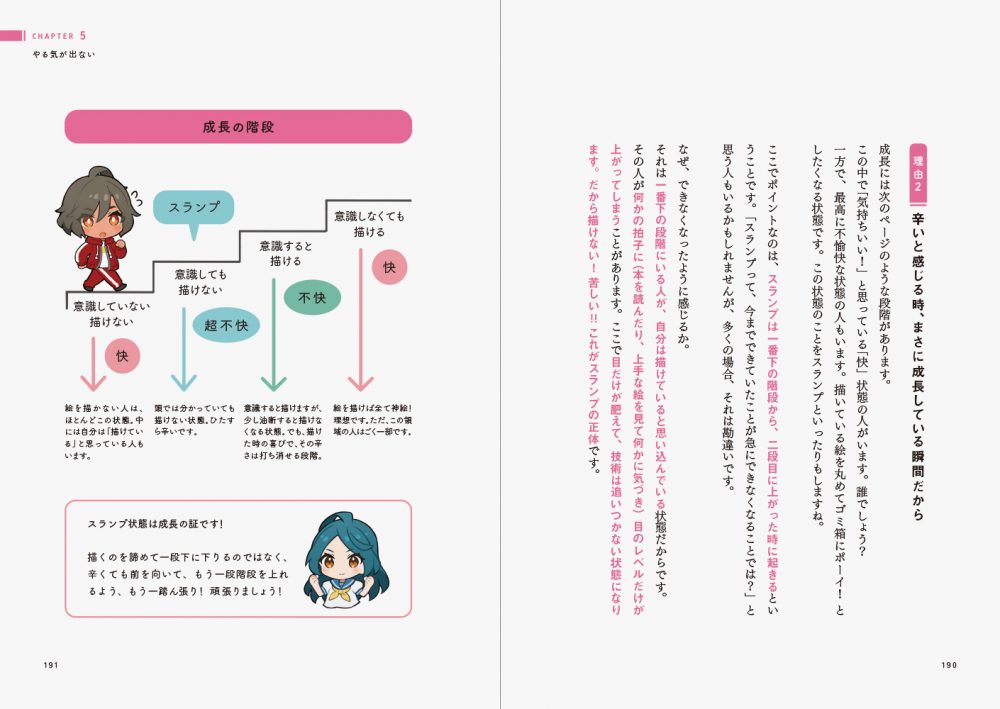
CHAPTER 5: I Can’t Get Motivated
CHAPTER 6: Things to Know About Product Manufacturing
This book is for everyone who draws!
This book is about the Naoki Saito method for getting better at drawing, which he talks about on his channel and which is gaining popularity. Themes are introduced by the major difficulties people have with drawing. There are many things that cause trouble or that are obstacles to drawing. However, if these obstacles can be overcome, drawing will be fun. And, because it’s fun, it will be easier to draw more, creating a virtuous cycle. So get rid of those worries and get joyful about expressing yourself!
Author/Illustrator
Naoki Saito is an illustrator born in 1982 from Yamagata Prefecture. After graduating from Tama Art University, Saito worked at a game company before becoming a freelancer. He also works as a coloring artist for the manga “BAKI”, and as the main illustrator for the game “Dragalia Lost” and also as an official card illustrator for Pokémon cards.
YouTube channel
Naoki Saito’s former YouTube channel had over 1,300,000 subscribers. In March 2023, it was wrongfully faced account banishment. He quickly restarted his new channel and on 24th April, he announced that from YouTube, he received his second silver certificate for passing 100,000 subscribers.
- Size:210×148mm
- Pages:224Pages(Full Color)
- Binding:Softbound
- Publisher:PIE International
- Language:Japanese
- ISBN:978-4-7562-5419-1 C2071
- Author:Naoki Saito
To check your neighbor bookstores, please click here.